随机数生成器：计算机是如何生成随机数的？

数千年以来，随机数已然成了人类文明重要见证者之一，我们对这个概念也不陌生，从古代巴比伦发明的彩票，到蒙特卡洛的轮盘，再到维加斯的骰子，它的目标就是帮助我们在未知情况下得到一个随机结果。

当然，除了赌博领域以外，随机数在数学、统计学、密码学，还有如今非常火的区块链等领域都发挥了不可磨灭的作用。但是工业时代之前，随机数可没现在这么风光，那时的人们只能使用的骰子、硬币之类的机械设备，生成随机的局限性也很大，想要生成一个随机数时通常也需要使用大量的时间和精力，到了如今计算机发达的今天，工具与方法已经焕然一新了。

产生随机数的方法

真随机数

模拟输入数字输出处理设备

随机数通常由随机数生成器（RNG，Random Numbers Generator）生成，人们想到的第一种 RNG 就是基于物理过程（如放射性衰变、光电效应、大气噪声）的某些特性转换为电信号的电子电路，再转换成可视的二进制数字 0 或 1，之后经过重复采样随机变化的信号，获得一系列随机数，如上图中模拟电子数字输出设备。

这种方式本质上和骰子、硬币这些媒介生成随机数的方式一样，处于计算机程序之外，但是可能性却有无限多，且理论上完全不可预测，因此被称作为硬件随机数生成器，也叫真随机数生成器（HRNG，Hardware True Random Numbers Generator）。

根据百科上的定义，真随机数是依赖于物理随机数生成器的。使用较多的就是电子元件中的噪音等较为高级、复杂的物理过程来生成。至于 “宇宙中不存在真正的随机” 这种言论已经属于哲学范畴，在此不做讨论。在此我们默认存在随机。

使用物理性随机数发生器生成的真随机数，可以说是完美再现了生活中的真正的 “随机”，也可以称为绝对的公平。

伪随机数

二进制攻击代码（1993年）

在计算机领域，我们使用的最多的还是伪随机数（Pseudo random number generator， PRNG）。为什么 “伪”，因为用这种方法生成的随机数通常由一个或多个初始值（也称为种子值或键）确定，当我们知道该初值和背后算法的工作原理之后，即可重现该 “随机结果”，所以用计算机随机函数所产生的 “随机数” 并不随机，是伪随机数。生成伪随机数的方法也称为伪随机数生成器。

从定义我们可以了解到，伪随机数其实是有规律的。PRNG 通过设定随机种子，从任意初始值开始生成。同样的初始值总是生成同样的随机序列，且 PRNG 既有周期性，一个周期表示一次重复的迭代，因此，周期越长的随机数更难预测和破解。

伪随机数生成算法

我们平时编码过程中使用的各编程语言都会内置生成随机数的 Random() 函数，该函数的底层会实现形式各异的随机数生成算法，但总会遵循如下这些基本规则：

接受一些初始输入数字，即种子或密钥。
应用该种子在数学运算的序列来生成结果，该结果就是随机数。
使用该结果随机数作为下一次迭代的种子。
重复该过程以模拟随机性（周期）。

我们以线性同余生成器为例。

线性同余生成器

该算法会产生一系列伪随机数。给定一个初始种子（seed）$X_0$ 和一个整数 a 作为其乘数（multiplier），同时，b 为增量（increment），m 为模量（modulus），生成函数可以表示为：**$X_n ≡（aX_{n-1} + b）mod m$，转换成编程的语法就是：$X_n =（a * X_{n-1} + b）％ m$**。

上述变量需要满足如下条件：

m > 0（模为正），
0 < a <m（乘数为正，且小于模数）
0 ≤ b < m（增量非负，且小于模量）
0 ≤ $X_0$ < m （种子非负，且小于模量）。

基于此，我们就可以写一个用于生成假随机数的函数了，如下这段 JavaScript 代码：

// x0 为种子，a 为乘数，b 为增量，m 为模，n随机序列长度
const linearRandomGenerator = (x0, a, b, m, n) => {
    const results = []
    for (let i = 0; i < n; i++) {
      x0 = (a * x0 + b) % m
        results.push(x0)
    }
    return results
}

线性同余生成器是最古老和最知名的伪随机序列生成器算法之一而可由计算机执行的随机数生成器算法，最早可以追溯到二十世纪四五十年代（如 Middle-square method 和 Lehmer random number generator），并一直沿用至今（Xoroshiro128 +，Squares RNG 等），感兴趣的同学可以阅读下面的延伸阅读和参考资料。

真随机数生成函数

之前已经介绍过，真随机数是使用物理设备产生的。我们可以从 Random.org 获得生成随机数的 API。这个网站免费提供真随机数的服务接口，并且可以自己设置上下限。

Random.org

那么，既然伪随机数生成那么简单，而且看上去确实是随机的，为什么人们还要大费周章的使用繁琐又高价的物理设备去获得随机数呢？

前面在伪随机数的定义里讲了，伪随机数其实是有周期的。

听起来很恐怖对不对？也就是说，经过足够多次的运行，结果会出现重复。

// Requires the GD Library
header("Content-type: image/png");
$im = imagecreatetruecolor(512, 512)
    or die("Cannot Initialize new GD image stream");
$white = imagecolorallocate($im, 255, 255, 255);
for ($y = 0; $y < 512; $y++) {
    for ($x = 0; $x < 512; $x++) {
        if (rand(0, 1)) {
            imagesetpixel($im, $x, $y, $white);
        }
    }
}		
imagepng($im);
imagedestroy($im);

上面代码摘自 Pseudo-Random Num.vs True Random Num，的一段代码，使用 PHP 语言编写的。它的作用就是将随机数可视化。下面分别放出真随机数和伪随机数的图像。

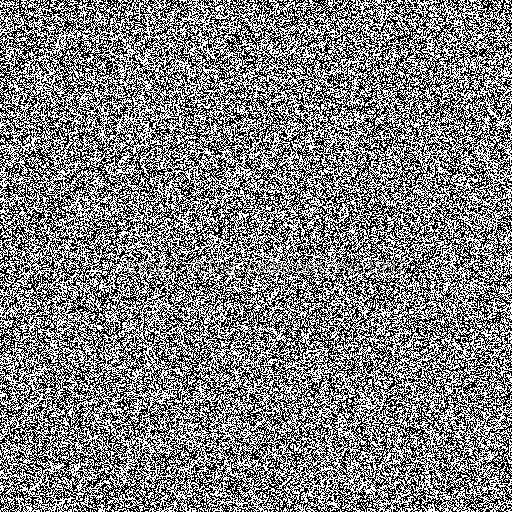
真随机数图像

伪随机数图像

很明显的可以看到，伪随机数的图像呈现出了某种规律。

因此，在很多需要保证绝对安全的系统中，真随机数的应用要大于伪随机数。

下面，我们就可以使用 Random.org 提供的 API，写出一个由大气噪声生成真随机数的函数，如下所示：

// 在用户输入上下限内生成随机数
const getRandom = async (min, max, base) => {
  const response = await 	fetch("https://www.random.org/integers/?num=1&min="+min+"
&max="+max+"&col=1&base="+base+"&format=plain&rnd=new")
        return response.text() 
}

该函数接受 min、max 参数分别设置随机数上下限，base 指定输出数格式（二进制、十进制或十六进制）。

我们还可以在页面中设置一个生成真随机数的交互按钮，但用户单击即会触发如下这段 handleGenerate() 函数：

<button onclick='handleGenerate()'>生成</button>

const handleGenerate = () => {
  // ...
	getRandom(minimum.value, maximum.value, base).then((data) => {
  	resultValue.textContent = data
		prompter.textContent = ""
  }).catch((error) => {
    resultValue.textContent = 'ERROR'
    prompter.textContent = '网络连接错误，无法生成随机数';
  })
}

最终，handleGenerate() 中就会调用 getRandom() 生成随机数并展示在页面中，如下：

该示例源代码：https://github.com/MeandNi/ang-example。

延伸阅读

https://blog.csdn.net/czc1997/article/details/78167705

https://zh.wikipedia.org/wiki/%E4%BC%AA%E9%9A%8F%E6%9C%BA%E6%80%A7

https://crypto.di.uoa.gr/CRYPTO.SEC/Randomness_Attacks_files/paper.pdf